Chapter 3
Getting Statistical: A Short Review of Basic Statistics
IN THIS CHAPTER
 Getting a handle on probability, randomness, sampling, and inference
Getting a handle on probability, randomness, sampling, and inference
 Tackling hypothesis testing
Tackling hypothesis testing
 Understanding nonparametric statistical tests
Understanding nonparametric statistical tests
This chapter provides an overview of basic concepts often taught in a one-term introductory statistics course. These concepts form a conceptual framework for the topics that we cover in greater depth throughout this book. Here, you get the scoop on probability, randomness, populations, samples, statistical inference, hypothesis testing, and nonparametric statistics.
Note: We only introduce the concepts here. They’re covered in much greater depth in Statistics For Dummies and Statistics II For Dummies, both written by Deborah J. Rumsey, PhD, and published by Wiley. Before you proceed, you may want to skim through this chapter to review the topics we cover so you can fill any gaps in your knowledge you may need in order to understand the concepts we introduce.
Taking a Chance on Probability
Defining probability is hard to do without using another word that means the same thing (or almost the same thing). Probability is the degree of certainty, the chance, or the likelihood that an event will occur. Unfortunately, if you then try to define chance or likelihood or certainty, you may wind up using the word probability in the definition. No worries — we clear up the basics of probability in the following sections. We explain how to define probability as a number and provide a few simple rules of probability. We also define odds, and compare odds to probability (because they are not the same thing).
Thinking of probability as a number
Probability describes the relative frequency of the occurrence of a particular event, such as getting heads on a coin flip or drawing the ace of spades from a deck of cards. Probability is a number between 0 and 1, although in casual conversation, you often see probabilities expressed as percentages. Probabilities are usually followed by the word chance instead of probability. For example: If the probability of rain is 0.7, you may hear someone say that there’s a 70 percent chance of rain.
- A probability of 0 (or 0 percent) means that the event definitely won’t occur.
- A probability of 1 (or 100 percent) means that the event definitely will occur.
- A probability between 0 and 1 (such as 0.7) means that — on average, over the long run — the event will occur some predictable part of the time (such as 70 percent of the time).
The probability of one particular event happening out of N equally likely events that could happen is 1/N. So with a deck of 52 different cards, the probability of drawing any one specific card (such as the ace of spades) compared to any of the other 51 cards is 1/52.
Following a few basic rules of probabilities
Here are three basic rules, or formulas, of probabilities. We call the first one the not rule, the second one the and rule, and the third one the or rule. In the formulas that follow, we use Prob as an abbreviation for probability, expressed as a fraction (between 0 and 1).
- The not rule: The probability of some event X not occurring is 1 minus the probability of X occurring, which can be expressed in an equation like this:
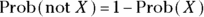
So if the probability of rain tomorrow is 0.7, then the probability of no rain tomorrow is 1 – 0.7, or 0.3.
- The and rule: For two independent events, X and Y, the probability of event X and event Y both occurring is equal to the product of the probability of each of the two events occurring independently. Expressed as an equation, the and rule looks like this:
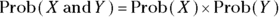
As an example of the and rule, imagine that you flip a fair coin and then draw a card from a deck. What’s the probability of getting heads on the coin flip and also drawing the ace of spades? The probability of getting heads in a fair coin flip is 1/2, and the probability of drawing the ace of spades from a deck of cards is 1/52. Therefore, the probability of having both of these events occur is 1/2 multiplied by 1/52, which is 1/104, or approximately 0.0096 (which is — as you can see — very unlikely).
- The or rule: For two independent events, X and Y, the probability of X or Y (or both) occurring is calculated by a more complicated formula, which can be derived from the preceding two rules. Here is the formula:
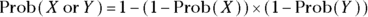
As an example, suppose that you roll a pair of six-sided dice. What’s the probability of rolling a 4 on at least one of the two dice? For one die, there is a 1/6 chance of rolling a 4, which is a probability of about 0.167. (The chance of getting any particular number on the roll of a six-sided die is 1/6, or 0.167.) Using the formula, the probability of rolling a 4 on at least one of the two dice is
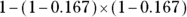 , which works out to
, which works out to 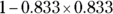 , or 0.31, approximately.
, or 0.31, approximately.
Comparing odds versus probability
You see the word odds used a lot in this book, especially in Chapter 13, which is about the fourfold cross-tab (contingency) table, and Chapter 18, which is about logistic regression. The terms odds and probability are linked, but they actually mean something different. Imagine you hear that a casino customer places a bet because the odds of losing are 2-to-1. If you ask them why they are doing that, they will tell you that such a bet wins — on average — one out of every three times, which is an expression of probability. We will examine how this works using formulas.

With a little algebra (which you don’t need to worry about), you can solve this formula for probability as a function of odds:

Returning to the casino example, if the customer says their odds of losing are 2-to-1, they mean 2/1, which equals 2. If we plug the odds of 2 into the second equation, we get 2/(1+2), which is 2/3, which can be rounded to 0.6667. The customer is correct — they will lose two out of every three times, and win one out of every three times, on average.
Table 3-1 shows how probability and odds are related.
TABLE 3-1 The Relationship between Probability and Odds
Probability |
Odds |
Interpretation |
|---|---|---|
1.0 |
Infinity |
The event will definitely occur. |
0.9 |
9 |
The event will occur 90% of the time (it is nine times as likely to occur as to not occur). |
0.75 |
3 |
The event will occur 75% of the time (it is three times as likely to occur as to not occur). |
0.5 |
1.0 |
The event will occur about half the time (it is equally likely to occur or not occur). |
0.25 |
0.3333 |
The event will occur 25% of the time (it is one-third as likely to occur as to not occur). |
0.1 |
0.1111 |
The event will occur 10% of the time (it is 1/9th as likely to occur as to not occur). |
0 |
0 |
The event definitely will not occur. |
Some Random Thoughts about Randomness
When discussing probability, it is also important to define the word random. Like the word probability, we use the word random all the time, and though we all have some intuitive concept of it, it is hard to define with precise language. In statistics, we often talk about random events and random variables. Random is a term that applies to sampling. In terms of a sequence of random numbers, random means the absence of any pattern in the numbers that can be used to predict what the next number will be.
Selecting Samples from Populations
Suppose that we want to know the average systolic blood pressure (SBP) of all the adults in a particular city. Measuring an entire population is called doing a census, and if we were to do that and calculate the average SBP in that city, we would have calculated a population parameter.
But the idea of doing a census to calculate such a parameter is not practical. Even if we somehow had a list of everyone in the city we could contact, it would be not be feasible to visit all of them and measure their SBP. Nor would it be necessary. Using inferential statistics, we could draw a sample from this population, measure their SBPs, and calculate the mean as a sample statistic. Using this approach, we could estimate the mean SBP of the population.
But drawing a sample that is representative of the background population depends on probability (as well as other factors). In the following sections, we explain why samples are valid but imperfect reflections of the population from which they’re drawn. We also describe the basics of probability distributions. For a more extensive discussion of sampling, see Chapter 6.
Recognizing that sampling isn’t perfect
- Population: All individuals in a defined target population. For example, this may be all individuals in the United States living with a diagnosis of Type II diabetes.
- Sample: A subset of the target population actually selected to participate in a study. For example, this could be patients in the United States living with Type II diabetes who visit a particular clinic and meet other qualification criteria for the study.
Any sample, no matter how carefully it is selected, is only an imperfect reflection of the population. This is due to the unavoidable occurrence of random sampling fluctuations called sampling error.
To illustrate sampling error, we obtained a data set containing the number of private and public airports in each of the United States and the District of Columbia in 2011 from Statista (available at https://www.statista.com/statistics/185902/us-civil-and-joint-use-airports-2008/). We started by making a histogram of the entire data set, which would be considered a census because it contains the entire population of states. A histogram is a visualization to determine the distribution of numerical data, and is described more extensively in Chapter 9. Here, we briefly summarize how to read a histogram:
- A histogram looks like a bar chart. It is specifically crafted to display a distribution.
- The histogram’s y-axis represents the number (or frequency) of individuals in the data that fall in the numerical ranges (known as classes) of the value being charted, which are listed across the x-axis. In this case, the y-axis would represent number of states falling in each class.
- This histogram’s x-axis represents classes, or numerical ranges of the value being charted, which is in this case is number of airports.
We first made a histogram of the census, then we took four random samples of 20 states and made a histogram of each of the samples. Figure 3-1 shows the results.

© John Wiley & Sons, Inc.
FIGURE 3-1: Distribution of number of private and public airports in 2011 in the population (of 50 states and the District of Columbia), and four different samples of 20 states from the same population.
As shown in Figure 3-1, when comparing the sample distributions to the distribution of the population using the histograms, you can see there are differences. Sample 2 looks much more like the population than Sample 4. However, they are all valid samples in that they were randomly selected from the population. The samples are an approximation to the true population distribution. In addition, the mean and standard deviation of the samples are likely close to the mean and standard deviation of the population, but not equal to it. (For a refresher on mean and standard deviation, see Chapter 9.) These characteristics of sampling error — where valid samples from the population are almost always somewhat different than the population — are true of any random sample.
Digging into probability distributions
As described in the preceding section, samples differ from populations because of random fluctuations. Because these random fluctuations fall into patterns, statisticians can describe quantitatively how these random fluctuations behave using mathematical equations called probability distribution functions. Probability distribution functions describe how likely it is that random fluctuations will exceed any given magnitude. A probability distribution can be represented in several ways:
- As a mathematical equation that calculates the chance that a fluctuation will be of a certain magnitude. Using calculus, this function can be integrated, which means turned into another related function that calculates the probability that a fluctuation will be at least as large as a certain magnitude.
- As a graph of the distribution, which looks and works much like a histogram.
- As a table of values indicating how likely it is that random fluctuations will exceed a certain magnitude.
In the following sections, we break down two types of distributions: those that describe fluctuations in your data, and those that you encounter when performing statistical tests.
Distributions that describe your data
Here are some common distributions that describe the random fluctuations found in data analyzed by biostatisticians:
- Normal: The familiar, bell-shaped, normal distribution is probably the most common distribution you will encounter. As an example, systolic blood pressure (SBP) is found to follow a normal distribution in human populations.
- Log-normal: The log-normal distribution is also called a skewed distribution. This distribution describes many laboratory results, such as enzymes and antibody titers, where most of the population tests on the low end of the scale. It is also the distribution seen for lengths of hospital stays, where most stays are 0 or 1 days, and the rest are longer.
- Binomial: The binomial distribution describes proportions, and represents the likelihood that a value will take one of two independent values (as whether an event occurs or does not occur). As an example, in a class held regularly where students can only pass or fail, the proportion who fail will follow a binomial distribution.
- Poisson: The Poisson distribution describes the number of occurrences of sporadic random events (rather than the binomial distribution, which is for more common events). Examples of where the Poisson distribution is used in biostatistics is where the events are not as common, such as deaths from specific cancers each year.
Chapter 24 describes these and other distribution functions in more detail, and you also encounter them throughout this book.
Distributions important to statistical testing
Some probability distributions don’t describe fluctuations in data values but instead describe fluctuations in calculated values as part of a statistical test (when you are calculating what’s called a test statistic). Distributions of test statistics include the Student t, chi-square, and Fisher F distributions. Test statistics are used to obtain the p values that result from the tests. See “Getting the language down” later in this chapter for a definition of p values.
Introducing Statistical Inference
Statistical inference is where you draw conclusions (or infer) about a population based on estimations from a sample from that population. The challenge posed by statistical inference theory is to extract real information from the noise in our data. This noise is made up of these random fluctuations as well as measurement error. This very broad area of statistical theory can be subdivided into two topics: statistical estimation theory and statistical decision theory.
Statistical estimation theory
Statistical estimation theory focuses how to improve the accuracy and precision of metrics calculated from samples. It provides methods to estimate how precise your measurements are to the true population value, and to calculate the range of values from your sample that’s likely to include the true population value. The following sections review the fundamentals of statistical estimation theory.
Accuracy and precision
- Accuracy refers to how close your measurement tends to come to the true value, without being systematically biased in one direction or another. Such a bias is called a systematic error.
- Precision refers to how close several replicate measurements come to each other — that is, how reproducible they are.
In estimation, both random and systematic errors reduce precision and accuracy. You cannot control random error, but you can control systematic error by improving your measurement methods. Consider the four different situations that can arise if you take multiple measurements from the same population:
- High precision and high accuracy is an ideal result. It means that each measurement you take is close to the others, and all of these are close to the true population value.
- High precision and low accuracy is not as ideal. This is where repeat measurements tend to be close to one another, but are not that close to the true value. This situation can when you ask survey respondents to self-report their weight. The average of the answers may be similar survey after survey, but the answers may be inaccurately lower than truth. Although it is easy to predict what the next measurement will be, the measurement is less useful if it does not help you know the true value. This indicates you may want to improve your measurement methods.
- Low precision and high accuracy is also not as ideal. This is where the measurements are not that close to one another, but are not that far from the true population value. In this case, you may trust your measurements, but find that it is hard to predict what the next one will be due to random error.
- Low precision and low accuracy shows the least ideal result, which is a low level of both precision and accuracy. This can only be improved through improving measurement methods.
Sampling distributions and standard errors
Fortunately, you don’t have to repeat the entire experiment a large number of times to calculate the SE. You can usually estimate the SE using data from a single experiment by using confidence intervals.
Confidence intervals
An important application of statistical estimation theory in biostatistics is calculating confidence intervals. Confidence intervals provide another way to indicate the precision of an estimate or measurement from a sample. A confidence interval (CI) is an interval placed around an estimated value to represent the range in which you strongly believe the true value for that variable lies. How wide you make this interval is dependent on a numeric expression of how strongly you believe the true value lie within it, which is called the confidence level (CL). If calculated properly, your stated confidence interval should encompass the true value a percentage of the time at least equal to the stated confidence level. In fact, if you are indeed making an estimate, it is best practices to report that estimate along with confidence intervals. As an example, you could express the 95 percent CI of the mean ages of a sample of graduating master’s degree students from a university this way: 32 years (95 percent CI 28 – 34 years).
At this point, you may be wondering how to calculate CIs. If so, turn to Chapter 10, where we describe how to calculate confidence intervals around means, proportions, event rates, regression coefficients, and other quantities you measure, count, or calculate.
Statistical decision theory
Statistical decision theory is a large branch of statistics that includes many subtopics. It encompasses all the famous (and many not-so-famous) statistical tests of significance, including the Student t tests and the analysis of variance (otherwise known as ANOVA). Both t tests and ANOVAs are covered in Chapter 11. Statistical decision theory also includes chi-square tests (explained in Chapter 12) and Pearson correlation tests (included in Chapter 16), to name a few.
- The average value of a measurement may be different in one group compared to another. For example, obese patients may have higher systolic blood pressure (SBP) measurements on average compared to non-obese patients. Another example is that the mean SBP of two groups of hypertensive patients may be different because each group is using a different drug — Drug A compared to Drug B. The difference between means in these groups is considered the effect size.
- The average value of a measurement may be different from zero (or from some other specified value). For example, the average reduction in pain level measurement in surgery patients from post-surgery compared to 30 days later may have an effect that is different from zero (or so we would hope)!
- Two numerical variables may be associated (also called correlated). For example, the taller people are on average, the more they weigh. When two variables like height and weight are associated in this way, the effect is called correlation, and is typically quantified by the Pearson correlation coefficient (described in Chapter 15).
Honing In on Hypothesis Testing
The theory of statistical hypothesis testing was developed in the early 20th century. Among other uses, it was designed to apply the scientific method to data sampled from populations. In the following sections, we explain the steps of hypothesis testing, the potential results, and possible errors that can be made when interpreting a statistical test. We also define and describe the relationships between power, sample size, and effect size in testing.
Getting the language down
Here are some of the most common terms used in hypothesis testing:
- Null hypothesis (abbreviated
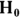 ): The assertion that any apparent effect you see in your data is not evidence of a true effect in the population, but is merely the result of random fluctuations.
): The assertion that any apparent effect you see in your data is not evidence of a true effect in the population, but is merely the result of random fluctuations. - Alternate hypothesis (abbreviated
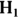 or
or 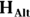 ): The assertion that there indeed is evidence in your data of a true effect in the population over and above what would be attributable to random fluctuations.
): The assertion that there indeed is evidence in your data of a true effect in the population over and above what would be attributable to random fluctuations. - Significance test: A calculation designed to determine whether
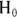 can reasonably explain what you see in your data or not.
can reasonably explain what you see in your data or not. - Significance: The conclusion that random fluctuations alone can’t account for the size of the effect you observe in your data. In this case,
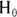 must be false, so you accept
must be false, so you accept 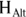 .
. - Statistic: A number that you obtain or calculate from your sample.
- Test statistic: A number calculated from your sample that is part of performing a statistical test. It can be for the purpose of testing
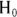 . In general, the test statistic is usually calculated as the ratio of a number that measures the size of the effect (the signal) divided by a number that measures the size of the random fluctuations (the noise).
. In general, the test statistic is usually calculated as the ratio of a number that measures the size of the effect (the signal) divided by a number that measures the size of the random fluctuations (the noise). - p value: The probability or likelihood that random fluctuations alone (in the absence of any true effect in the population) can produce the effect observed in your sample (or, at least as large as the effect you observe in your sample). The p value is the probability of random fluctuations making the test statistic at least as large as what you calculate from your sample (or, more precisely, at least as far away from
 in the direction of
in the direction of 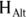 ).
). - Type I error: Choosing that
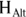 is correct when in fact, no true effect above random fluctuations is present.
is correct when in fact, no true effect above random fluctuations is present. - Alpha (α): The probability of making a Type I error.
- Type II error: Choosing that
 is correct when in fact there is indeed a true effect present that rises above random fluctuations.
is correct when in fact there is indeed a true effect present that rises above random fluctuations. - Beta (β): The probability of making a Type II error.
- Power: The same as 1 – β, which is probability of choosing
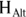 as correct when in fact there is a true effect above random fluctuations present.
as correct when in fact there is a true effect above random fluctuations present.
Testing for significance
Reduce your raw sample data down into a single number called a test statistic.
Each test statistic has its own formula, but in general, the test statistic represents the magnitude of the effect you’re looking for relative to the magnitude of the random noise in your data. For example, the test statistic for the unpaired Student t test for comparing means between two groups is calculated as a fraction:
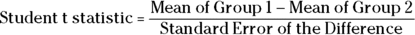
The numerator is a measure of the effect, which is the mean difference between the two groups. And the denominator is a measure of the random noise in your sample, which is represented by the spread of values within each group. Thinking about this fraction philosophically, you will notice that the larger the observed effect is (numerator) relative to the amount of random noise in your data (denominator), the larger the Student t statistic will be.
Determine how likely (or unlikely) it is for random fluctuations to produce a test statistic as large as the one you actually got from your data.
To do this, you use complicated formulas to generate the test statistic. Once the test statistic is calculated, it is placed on a probability distribution. The distribution describes how much the test statistic bounces around if only random fluctuations are present (that is, if
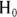 is true). For example, the Student T statistic is placed on the Student T distribution. The result from placing the test statistic on a distribution is known as the p value, which is described in the next section.
is true). For example, the Student T statistic is placed on the Student T distribution. The result from placing the test statistic on a distribution is known as the p value, which is described in the next section.
Understanding the meaning of “p value” as the result of a test
The end result of a statistical significance test is a p value, which represents the probability that random fluctuations alone could have generated results. If that probability is medium to high, the interpretation is that the null hypothesis, or 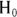 , is correct. If that probability is very low, then the interpretation is that we reject the null hypothesis, and accept the alternate hypothesis (
, is correct. If that probability is very low, then the interpretation is that we reject the null hypothesis, and accept the alternate hypothesis (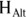 ) as correct. If you find yourself rejecting the null, you can say that the effect seen in your data is statistically significant.
) as correct. If you find yourself rejecting the null, you can say that the effect seen in your data is statistically significant.
Examining Type I and Type II errors
The outcome of a statistical test is a decision to either accept the 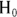 , or reject
, or reject 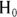 in favor of
in favor of 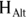 . Because
. Because 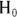 pertains to the population’s true value, the effect you see in your sample is either true or false for the population from which you are sampling. You may never know what that truth is, but an objective truth is out there nonetheless.
pertains to the population’s true value, the effect you see in your sample is either true or false for the population from which you are sampling. You may never know what that truth is, but an objective truth is out there nonetheless.
The truth can be one of two answers — the effect is there, or the effect is not there. Also, your conclusion from your sample will be one of two answers — the effect is there, or the effect is not there.
- Your test is not statistically significant, and H0is true. This is an ideal situation because the conclusion of your test matches the truth. If you were testing the mean difference in effect between Drug A and Drug B, and in truth there was no difference in effect, if your test also was not statistically significant, this would be an ideal result.
- Your test is not statistically significant, but H0is false. In this situation, the interpretation of your test is wrong and does not match truth. Imagine testing the difference in effect between Drug C and Drug D, where in truth, Drug C had more effect than Drug D. If your test was not statistically significant, it would be the wrong result. This situation is called Type II error. The probability of making a Type II error is represented by the Greek letter beta (β).
- Your test is statistically significant, and HAltis true. This is another situation where you have an ideal result. Imagine we are testing the difference in effect between Drug C and Drug D, where in truth, Drug C has more of an effect. If the test was statistically significant, the interpretation would be to reject H0, which would be correct.
- Your test is statistically significant, but HAltis false. This is another situation where your test interpretation does not match the truth. If there was in truth no difference in effect between Drug A and Drug B, but your test was statistically significant, it would be incorrect. This situation is called Type I error. The probability of making a Type I error is represented by the Greek letter alpha (α).
At this point, you may be wondering, “Is there any way to keep both Type I and Type II error small?” The answer is yes, and it involves power, which is described in the next section.
Grasping the power of a test
The power of any statistical test depends on several factors:
- The α level you’ve established for the test — that is, the chance you’re willing to accept making a Type I error (usually 0.05)
- The actual magnitude of the effect in the population, relative to the amount of noise in the data
- The size of your sample
Power, sample size, effect size relative to noise, and α level can’t all be varied independently. They’re interrelated, because they’re connected and constrained by a mathematical relationship involving all four quantities.
This relationship between power, sample size, effect size relative to noise, and α level is often very complicated, and it can’t always be written down explicitly as a formula. But the relationship does exist. As evidence of this, for any particular type of test, theoretically, you can determine any one of the four quantities if you know the other three. So for each statistical test, there are four different ways to do power calculations, with each way calculating one of the four quantities from arbitrarily specified values of the other three. (We have more to say about this in Chapter 5, where we describe practical issues that arise during the design of research studies.) In the following sections, we describe the relationships between power, sample size, and effect size, and briefly review how you can perform power calculations.
Power, sample size, and effect size relationships
Power versus sample size, for various effect sizes: For all statistical tests, power always increases as the sample size increases, if the other variables including α level and effect size are held constant. This relationship is illustrated in Figure 3-2. “Eff” is the effect size — the between-group difference divided by the within-group standard deviation.
Small samples will not be able to produce significant results unless the effect size is very large. Conversely, statistical tests using extremely large samples including many thousands of participants are almost always statistically significant unless the effect size is near zero. In epidemiological studies, which often involve hundreds of thousands of subjects, statistical tests tend to produce extremely small (and therefore extremely significant) p values, even when the effect size is so small that it’s of no practical importance (meaning it is clinically insignificant).

© John Wiley & Sons, Inc.
FIGURE 3-2: The power of a statistical test increases as the sample size and the effect size increase.
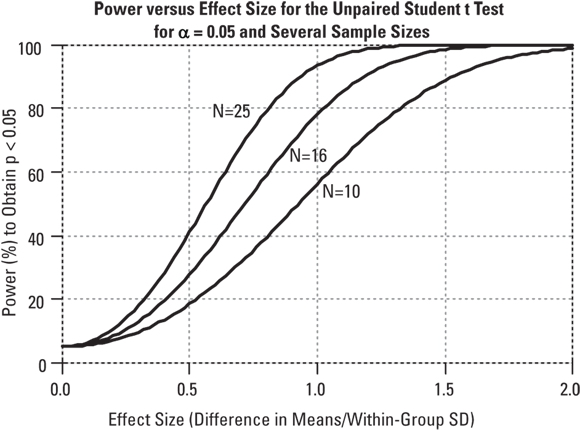
Power versus effect size, for various sample sizes: For all statistical tests, power always increases as the effect size increases, if other variables including the α level and sample size are held constant. This relationship is illustrated in Figure 3-3. “N” is the number of participants in each group.
© John Wiley & Sons, Inc.
FIGURE 3-3: The power of a statistical test increases as the effect size increases.
For very large effect sizes, the power approaches 100 percent. For very small effect sizes, you may think the power of the test would approach zero, but you can see from Figure 3-3 that it doesn’t go down all the way to zero. It actually approaches the α level of the test. (Keep in mind that the α level of the test is the probability of the test producing a significant result when no effect is truly present.)
Sample size versus effect size, for various values of power: For all statistical tests, sample size and effect size are inversely related, if other variables including α level and power are held constant. Small effects can be detected only with large samples, and large effects can often be detected with small samples. This relationship is illustrated in Figure 3-4.
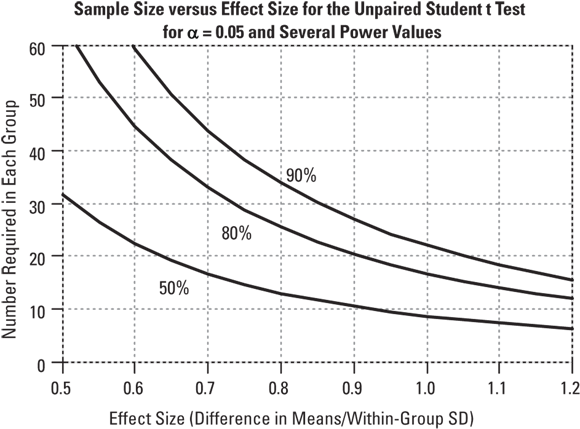
© John Wiley & Sons, Inc.
FIGURE 3-4: Smaller effects need larger samples.
This inverse relationship between sample size and effect size takes on a very simple mathematical form (at least to a good approximation): The required sample size is inversely proportional to the square of the effect size that can be detected. Or, equivalently, the detectable effect size is inversely proportional to the square root of the sample size. So, quadrupling your sample size allows you to detect effect sizes only one-half as large.
How to do power calculations
- Computer software: The larger statistics packages such as SPSS, SAS, and R enable you to perform a wide range of power calculations. Chapter 4 describes these different packages. There are also programs specially designed for conducting power calculations, such as PS and G*Power, which are described in Chapter 4.
- Web pages: Many of the more common power calculations can be performed online using web-based calculators. An example of one of these is here:
https://clincalc.com/stats/samplesize.aspx. - Rules of thumb: Some approximate sample-size calculations are simple enough to do on a scrap of paper or even in your head! You find some of these in Chapter 25.
Going Outside the Norm with Nonparametric Statistics
All statistical tests are derived on the basis of some assumptions about your data. Most of the classical significance tests, including Student t tests, analysis of variance (ANOVA), and regression tests, assume that your data are distributed according to some classical sampling distribution, which is also called a frequency distribution. Most tests assume your data has a normal distribution (see Chapter 24). Because the classic distribution functions are all written as mathematical expressions involving parameters (like means and standard deviation), they’re called parametric distribution functions.
Parametric tests assume that your data conforms to a parametric distribution function. Because the normal distribution is the most common statistical distribution, the term parametric test is often used to mean a test that assumes normally distributed data. But sometimes your data don’t follow a parametric distribution. For example, it may be very noticeably skewed, as shown in Figure 3-5a.
Sometimes, you may be able to perform a mathematical transformation of your data to make it more normally distributed. For example, many variables that have a skewed distribution can be turned into normally distributed numbers by taking logarithms, as shown in Figure 3-5b. If, by trial and error, you can find some kind of transformation that normalizes your data, you can run the classical tests on the transformed data, as described in Chapter 9.
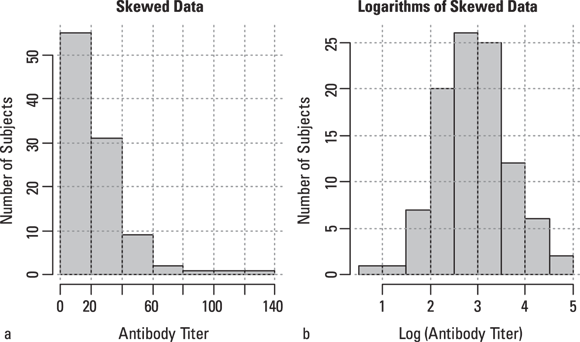
© John Wiley & Sons, Inc.
FIGURE 3-5: Skewed data (a) can sometimes be turned into normally distributed data (b) by taking logarithms.
But sometimes your data are not normally distributed, and for whatever reason, you give up on trying to do a parametric test. Maybe you can’t find a good transformation for your data, or maybe you don’t want to have to undo the transformation in order to do your interpretation, or maybe you simply have too small of a sample size to be able to perceive a clear parametric distribution when you make a histogram. Fortunately, statisticians have developed other tests that you can use that are not based on the assumption your data are normally distributed, or have any parametric distribution. Unsurprisingly, these are called nonparametric tests. Most of the common classic parametric tests have nonparametric counterparts you can use as an alternative. As you may expect, the most widely known and commonly used nonparametric tests are those that correspond to the most widely known and commonly used classical tests. Some of these are shown in Table 3-2.
TABLE 3-2 Nonparametric Counterparts of Classic Tests
Classic Parametric Test |
Nonparametric Equivalent |
|---|---|
One-group or paired Student t test (see Chapter 11) |
Wilcoxon Signed-Ranks test |
Two-group Student t test (see Chapter 11) |
Mann-Whitney U test |
One-way ANOVA (see Chapter 11) |
Kruskal-Wallis test |
Pearson Correlation test (see Chapter 15) |
Spearman Rank Correlation test |
Most nonparametric tests involve first sorting your data values, from lowest to highest, and recording the rank of each measurement. Ranks are like class ranks in school, where the person with the highest grade point average (GPA) is ranked number 1, and the person with the next highest GPA is ranked number 2 and so on. Ranking forces each individual to be separated from the next by one unit of rank. In data, the lowest value has a rank of 1, the next highest value has a rank of 2, and so on. All subsequent calculations are done with these ranks rather than with the actual data values. However, using ranks instead of the actual data loses information, so you should avoid using nonparametric tests if your data qualify for parametric methods.
Although nonparametric tests don’t assume normality, they do make certain assumptions about your data. For example, many nonparametric tests assume that you don’t have any tied values in your data set (in other words, no two participants have exactly the same values). Most parametric tests incorporate adjustments for the presence of ties, but this weakens the test and makes the results less exact.
 Probabilities are numbers between 0 and 1 that can be interpreted this way:
Probabilities are numbers between 0 and 1 that can be interpreted this way:  Don’t use percentage numbers (0 to 100) in probability formulas.
Don’t use percentage numbers (0 to 100) in probability formulas. We discussed setting α = 0.05, meaning that you are willing to tolerate a Type I error rate of 5 percent. Theoretically, you could change this number. You can increase your chance of making a Type I error by increasing your α from 0.05 to a higher number like 0.10, which is done in rare situations. But if you reduce your α to number smaller than 0.05 — like 0.01, or 0.001 — then you run the risk of never calculating a test statistic with a p value that is statistically significant, even if a true effect is present. If α is set too low, it means you are being very picky about accepting a true effect suggested by the statistics in your sample. If a drug really is effective, you want to get a result that you interpret as statistically significant when you test it. What this shows is that you need to strike a balance between the likelihood of committing Type I and Type II errors — between the α and β error rates. If you make α too small, β will become too large, and vice versa.
We discussed setting α = 0.05, meaning that you are willing to tolerate a Type I error rate of 5 percent. Theoretically, you could change this number. You can increase your chance of making a Type I error by increasing your α from 0.05 to a higher number like 0.10, which is done in rare situations. But if you reduce your α to number smaller than 0.05 — like 0.01, or 0.001 — then you run the risk of never calculating a test statistic with a p value that is statistically significant, even if a true effect is present. If α is set too low, it means you are being very picky about accepting a true effect suggested by the statistics in your sample. If a drug really is effective, you want to get a result that you interpret as statistically significant when you test it. What this shows is that you need to strike a balance between the likelihood of committing Type I and Type II errors — between the α and β error rates. If you make α too small, β will become too large, and vice versa.